Finland: Regions
Transverse Mercator projection
This map uses Transverse Mercator projection. But what is a Transverse and what is projection? Well, lets start about what a projection actually is...
Map projection. Map projection is a way to represent the globe which is an inperfect sphere, onto a flat survace. (For example a large piece of paper or the screen you are currently watching ;-)) And why? Well in order to get a useable map. And that last part, well that is the hard part. You have to deal with the practival use of maps (navigation, geograpgical shapes, distance between objects, etc) as well as very complicated mathematical problems about how to shape the world. As you must surely understand, there is not one answer to this problem. Any 2D projection of the world will always distort the reality in some smaller or larger way. Because every problem has it's own solution, there are numerous amounts of projections. Each was developed to minimize the disortion for that specific use. Some are very famous, some you will probably never have heard from. Maybe click around the globe on mapclicker and find the obscure one you where looking for.
J.H. Lambert
Johann Heinrich Lambert was born in Mulhouse in France and was a German/Swiss scientist. He did more than creating maps, he was also a mathematician, an astronomer, physicist and philosopher. You could say he was quite the cool guy, mostly because he was the first that proofed that pi (3,14∞) is an irrational number. That means you cannot write pi as a fraction. Lambert is seen as the founder of modern cartography with his theory of map projections. The most famous and widely used is LAEA (used for Oceania). Other widely used projections from Lambert are LCC (used for Canada) and Transeverse Mercator (used for Finland).
 Mercator
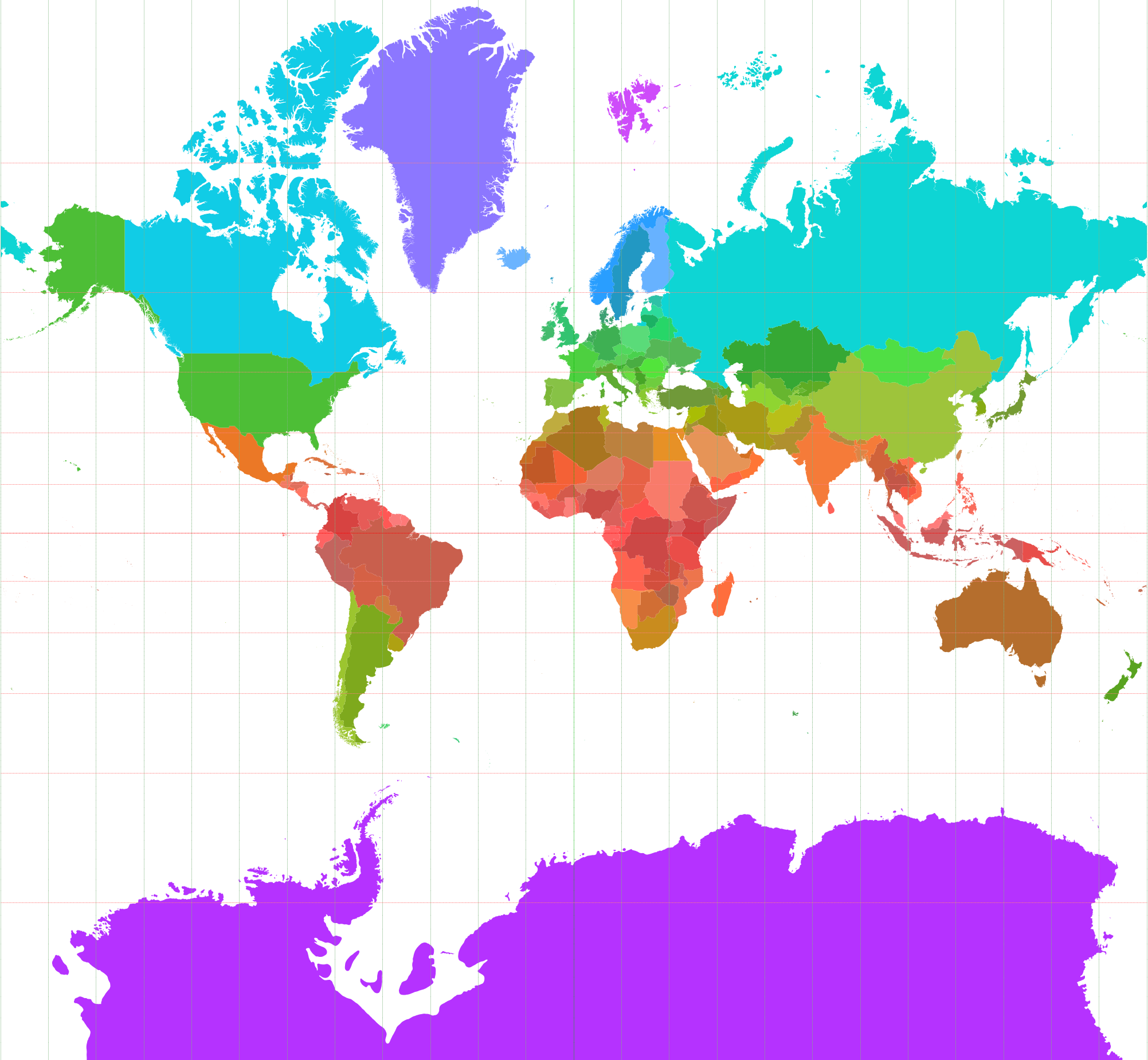
Mercator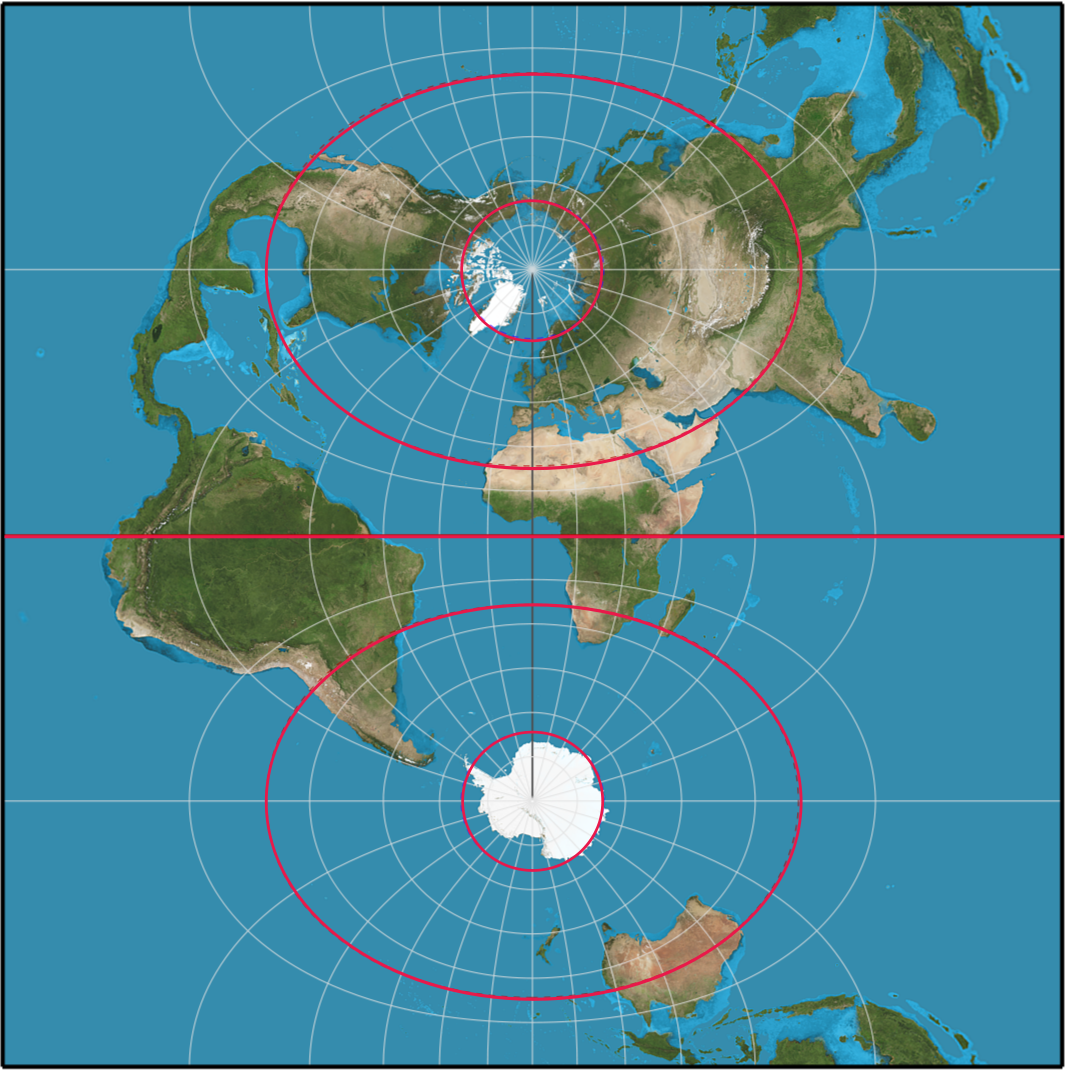 Transverse Mercator
Transverse MercatorTransverse Mercator
As shown in the example above, the difference between Mercator and Transverse Mercator is the central axis. They do however share the same underlying construction and therefore the transverse Mercator has many of the same traits. They are for example both cylindrical and they are both conformal, which means that the point scale is not dependent on direction and that the local shapes are well maintained.

J.H. Lambert

Transverse Mercator world map
