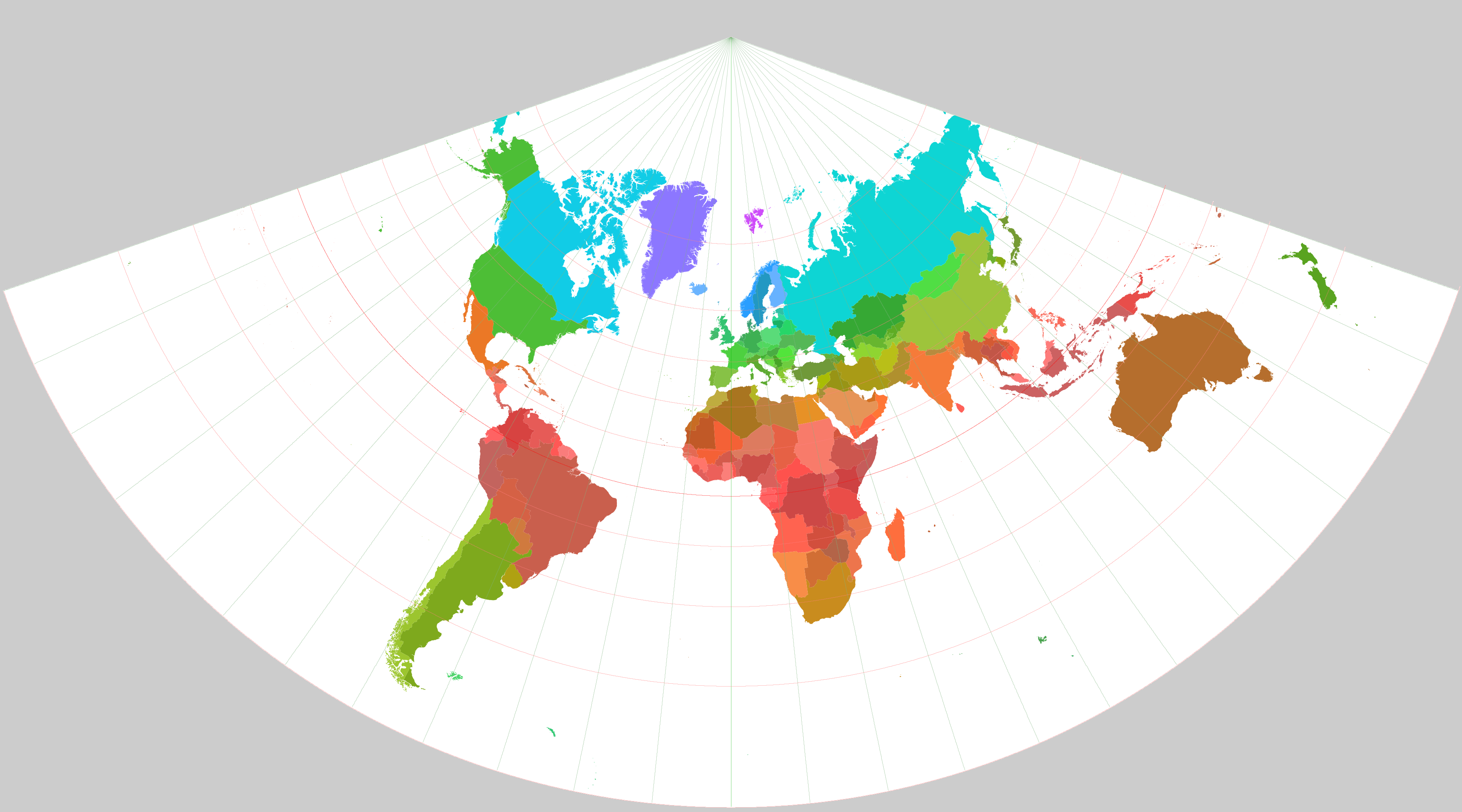
Canada Provinces and Territories
Lambert conformal conic projection (LCC)
This map uses A Lambert conformal conic projection. But what is a Lambert, or an conformal and what is projection? Well, lets start about what a projection actually is...
Map projection. Map projection is a way to represent the globe which is an inperfect sphere, onto a flat survace. (For example a large piece of paper or the screen you are currently watching ;-)) And why? Well in order to get a useable map. And that last part, well that is the hard part. You have to deal with the practival use of maps (navigation, geograpgical shapes, distance between objects, etc) as well as very complicated mathematical problems about how to shape the world. As you must surely understand, there is not one answer to this problem. Any 2D projection of the world will always distort the reality in some smaller or larger way. Because every problem has it's own solution, there are numerous amounts of projections. Each was developed to minimize the disortion for that specific use. Some are very famous, some you will probably never have heard from. Maybe click around the globe on mapclicker and find the obscure one you where looking for.
J.H. Lambert
Johann Heinrich Lambert was born in Mulhouse in France and was a German/Swiss scientist. He did more than creating maps, he was also a mathematician, an astronomer, physicist and philosopher. You could say he was quite the cool guy, mostly because he was the first that proofed that pi (3,14∞) is an irrational number. That means you cannot write pi as a fraction. Lambert is seen as the founder of modern cartography with his theory of map projections. The most famous and widely used is LAEA (used for Oceania). Other widely used projections from Lambert are LCC (used for Canada) and Transeverse Mercator (used for Finland).
LCC
The Lambert conformal conic projection (LCC) is commenly used method to display part of the world on a flat surface. The conic part of the name gives away the specific method used. A cone is put around the earth, where the cone cuts the ellipsoid of the earth on two paralel lines. From the center of the earth the globe is projected onto the cone, which when unwrapped forms the actual map. Near the two used paralels, distortion is minimal, but when moving further away from the main paralels distortion is amplyfied.
This projection is conformal, in this specific projection this means that the angles on the map are the as in reality. Using the Pythagorean theorem it is easy to calculate distances on the map.
 LCC map example
LCC map example
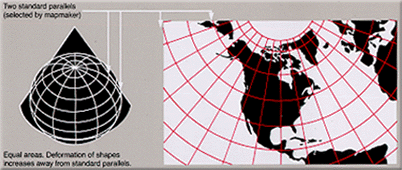 Cone over the globe
Cone over the globe
